개인사
BFS 너비 우선 탐색 C++ 본문
728x90
개요
그래프 : 노드와 간선으로 이루어진 자료구조
완전 탐색 : 특정 노드에서 갈 수 있는 모든 노드를 확인하는 방법
DFS : 깊이 우선 탐색
BFS(Breadth First Search) : 넓이 우선 탐색 -> 가까운/인접한 노드부터 탐색 즉, 발견되는 노드부터 탐색한다.
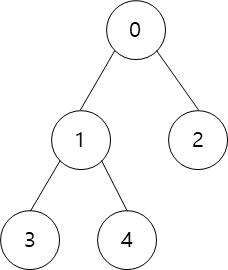
위 그래프를 DFS로 탐색 한다면 0 -> 1 - > 3 -> 4 -> 2 순으로 탐색하게 된다. (깊이 우선)
BFS로 탐색한다면 결과는 0 -> 1 -> 2 -> 3 -> 4 가 될 것이다. (넓이 우선, 가까운것 부터 탐색)
BFS 진행 방식
- 대기열 준비(Queue 자료 구조를 선택)
- 시작 노드에 큐 삽입
- 큐(대기열)에 맨 앞 노드부터 추출 및 확인(now) | 실제 탑승
- now를 기준으로 연결되어 있는 노드들을 큐에 등록(next 후보 검색)
- next 후보들을 큐에 등록
- 큐(대기열)이 사라지거나, 원하는 값을 찾을 때 까지 모든 노드를 확인할 때 까지 3 ~ 5번 계속 반복
예제
1. 복잡한 그래프

위 그래프에서 0번 노드를 루트로 가정하고 본다면 level은 다음과 같이 나눌 수 있다.
- level 0 : 0
- level 1 : 1, 2, 3, 4
- level 2 : 5, 6, 8
- level 3 : 7
그래프의 인접 리스트가 오름차순으로 정렬된 상태라고 가정할 때 DFS와 BFS의 탐색 순서는 다음과 같다.
DFS : 0 -> 1 -> 2 -> 8 -> 3 -> 4 -> 5 -> 6 -> 7
BFS : 0 -> 1 -> 2 -> 3 -> 4 -> 8 -> 5 -> 6 -> 7
이는 루트가 0일때의 가정이고 루트를 다른 노드로 변경하여도 충분히 탐색을 진행할 수 있다.
2. 코드를 작성해 보자
위 그래프를 하드 코딩해 주고, 출발할 특정 노드 n을 입력받아 해당 노드로 부터 넓이 우선 탐색을 진행하자.
코드
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
vector<vector<int>> nodes = { // 노드의 연결 정보를 하드 코딩 해준다.
{1, 2, 3, 4},
{0},
{0, 8},
{0},
{0, 5, 6},
{4},
{4, 7},
{6},
{2}
};
void bfs(int start_node) {
queue<int> q; // 큐 생성 및 시작 노드를 넣어준다.
q.push(start_node);
int v[9] = { 0, }; // 방문 처리 배열 생성
v[start_node] = 1; // 시작 노드 방문 처리
cout << start_node << " "; // 시작 노드부터 출력
while (!q.empty()) {
int current_num = q.front(); q.pop();
for (int i = 0; i < nodes[current_num].size(); i++) { // 현재 노드에서 인접한 노드들 탐색
if (v[nodes[current_num][i]]) continue; // 현재 탐색중인 노드의 방문 체크
v[nodes[current_num][i]] = 1; // 방문 처리
cout << nodes[current_num][i] << " "; // 출력
q.push(nodes[current_num][i]); // 큐에 해당 노드 삽입
}
}
}
int main() {
int n;
cin >> n;
bfs(n); // 입력 받은 노드로 부터 BFS
}
입력
0
출력
0 1 2 3 4 8 5 6 7
입력
5
출력
5 4 0 6 1 2 3 7 8728x90
'알고리즘 공부 > 알고리즘' 카테고리의 다른 글
| 최소 신장 트리 MST, Union-Find C++ (0) | 2024.08.13 |
|---|---|
| 유니온 파인드 Union-Find C++ (0) | 2024.08.13 |
| 그래프, 트리, DFS C++ (0) | 2024.07.31 |
| 백트래킹(2) 순열, 조합, N Castle C++ (0) | 2024.07.30 |
| 백트래킹 C++ (0) | 2024.07.29 |




